SYSTEM-LEVEL AND PER-CHANNEL TUNING
The default tuning and configuration for a new Patch Bank is 12-Tone Equal Temperament, with A4 set to 440 Hz, at note number 69. If you are not interested in any other tuning, you can leave this set as-is and never worry about tuning again :).
The Isle I-1 includes over 125 canned tuning algorithms, each of which may be used out-of-the-box, further configured, or totally customized. (You know the old joke, “You can can a tuning, but you can’t tune a synth.” Maybe not.) Tunings associate keys/note numbers with an initial frequency for sound generation; the engine and its internal algorithms work entirely in frequency, though a performer is usually working with an instrument of some sort, and prefers to work within a common musical language/system and deal with a much smaller, more manageable set of notes. In the Isle I-1, tunings also define note names for the given system (you may set an Oscillator to always use a given note from the tuning, regardless of the note played) and named intervals (rather than dealing with frequency ratios, a number of octaves, or a number of semitones, you may find it easier/convenient to say “up a major 3rd”).
Tunings are usually set at the system level, but may be set for an individual control (MIDI) channel. You may be modelling an ensemble over multiple channels, where most of the instruments share 12-Tone Equal Temperament, but a single channel may be reserved for modelling steel drums, or a kalimba, or a bonang, and for accuracy, uses its own tuning. Or you may be trying to compose a demo for a software synthesizer you developed, and wanted a section that uses Ligeti-style tone clusters, but wanted them to sound different, and thought that a different tuning system would help on that front. These are use cases for setting a channel to its own tuning.
WHAT IS A TUNING?
Sound is a set of vibrations occurring over time. These vibrations occur over some physical medium – usually air, when we’re talking about the mammalian sense of hearing, though the medium could be water, a lake of mercury, or a string coated in wax and connecting two empty cans. When these vibrations happen with a more-or-less repeated wave form, we hear the speed of these vibrations as pitch. Counting the vibrations over a unit of time gives us the ability to measure, discuss, and perform math/develop theory about such vibrations. Typically, waveforms are measured in units of waves per second, or Hertz (Hz) (the measurement itself is called “frequency”). Practically all of the math related to sound, from generation of a sine wave to synthesis algorithms to the Fourier transform, works on units of Hertz. To “play a note” means to trigger a pitched sound, vibrating at a frequency.
There is an infinite number of frequencies, even when limiting the range of frequencies to the range perceptible by humans. Further complicating matters, what we hear as a linear progression of pitch as it increases is actually an exponential increase in frequency. A pitch that we hear as one octave higher than another is double the frequency of the lower pitch; two octaves higher is 4x the lower. Ultimately, people are bad at precision; we are much better at sensing simple relationships – half as long, twice as loud. All of this makes thinking about, discussing, or constructing music difficult and cumbersome if we try to do so in units of Hertz. We tend to better recognize and construct patterns in sounds if we use a smaller and consistent set of frequencies as the basis of a music. It is also much simpler to communicate about these patterns if we give simpler names to the members of this small subset. If harmony is an important consideration (it doesn’t have to be), it is also convenient to name the distances between two simultaneous pitches, and stacks of simultaneous pitches. Whether such components are defined by one person for a single piece of music, honed by a culture over centuries, or given by divinity, these are the beginnings of a “system” of music.
Selection of a set of frequencies, or scale construction, is usually done according to a set of rules, or at least, guidelines. Octaves feature prominently in most historic approaches to scale construction, as we hear octaves as far-and-away the most consonant interval, and we tend to hear integer-power-of-2 multiples of a frequency as “the same note” (octave equivalence). (Note that octaves are not the only interval by which to define a scale.) A scale consisting only of octave-equivalent multiples of a single pitch, however, does not produce particularly interesting or compelling music, so other pitches are chosen at different points across the octave. The rules for choosing these pitches may be as complex and mathematically precise as, “this is how to divide the syntonic comma across all of the pitches in the scale, and that gives an equal division of the octave into however many steps, for a ratio of each scale step of the nth-root-of-2,” or as simple as, “this is the way we’ve always done it here.”
Scale construction, however, is only one part of building a tuning. As a great many humans are not gifted with a singing voice which others particularly want to hear, we’ve invented instruments over the course of human history which can produce pitched sounds by purely mechanical means. The other aspect of a tuning is selection and placement of pitches from the complete, infinite set of notes defined in either direction by the rules of scale construction. Consider the following examples:
Flutes and other wind instruments produce pitches by stopping holes drilled into different places along a hollow tube, effectively making the tube vibrate as though its length were constantly changing. The placement of these holes, relative to the overall length of the tube, gives these instruments an intonation, while the compact size of the tube and closeness of the holes make it easy to play with human hands. Different lengths and widths of tube produce instruments which excel across a certain range of pitches, might be able to reach others without sounding quite as great, and are totally unable to play pitches above or below its range – this is the difference between a flute, a clarinet, an oboe, and a bassoon.
A stringed instrument, such as guitar, requires a bit more work to get into tune – you have to tighten strings of varying thickness, some wound and others unwound, to produce exactly the intended pitch. Frets stop each string at a point somewhere along the length of the string, effectively shortening the length of vibrating string and creating an intonation. On a guitar, there are multiple places to play the same note in the same octave, but each of these places gives a slightly different timbre, due to strings being wound or unwound, open or stopped. The standard way of tuning a guitar is to tune the lowest string to the E below middle C, then ascending mostly in 4ths to A, D, G, B, and an E 2 octaves above the low string. However, often guitarists use different tunings for different reasons – a guitarist might tune to make a D-minor chord out of the open strings, reaching a low D which would not otherwise be available. In this tuning, many of the strings are a bit more slack than in standard tuning, and vibrate differently to give a slightly different character; the tuning also makes some patterns easier to play than in standard tuning, though others which are easy to play in standard tuning are now more difficult. While, in both tunings, the guitar is in 12-tone equal temperament, and thus the scale is not constructed any differently, the notes are arranged differently.
In the MIDI age, while many MIDI controllers arrange keys in the familiar “Halberstadt” keyboard pattern popularized by pianos, a device such as the Novation LaunchPad is just a rectangular grid of buttons which can be mapped at will. There is no preconceived notion of which notes should be assigned to which button in the grid; the arrangement can be left to the performer, who might not even map the notes in sequential order – perhaps the arrangement of pitches in one row might map to a single chord, excluding notes which are not a part of the chord, while the next row maps a completely different chord, though containing one or two notes included in the first.
In all of these cases – construction of woodwind instruments, an alternate tuning of a guitar, the mapping of LaunchPad buttons to specific notes – performance and aesthetic considerations influence the choice of notes available on an instrument, as well as the arrangement of available notes across the instrument. This is also part of an instrument’s overall tuning.
BASIC ISLE I-1 TUNING CONCEPTS AND PARAMETERS
Tunings, as well as all system settings, are stored with the Patch Bank. This approach allows each Patch Bank to specify, save, and reload its own Tuning system, and not force you to remember your tuning settings from the last time you used it. The system-level Tuning affects, as its name implies, the entire system. However, each MIDI control channel can specify its own tuning (though by default they are locked to the system tuning).
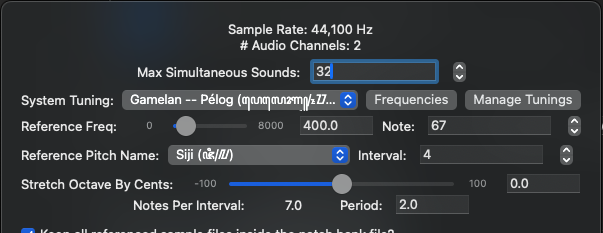
Selecting a tuning is pretty straightforward – in the system-level view at the bottom of the main window, click the settings icon next to the “System-Level Oscillators” button. This opens a popover with system-level info, including the system-level tuning. You will also see all subscribed MIDI channels – they may be locked to the system tuning (by selecting the Lock to System Tuning checkbox), but may specify their own tuning. The common settings are available in both places, and operate identically.
Choose a tuning system from the drop-down list. Available tunings are any of the 25 broad categories of canned tunings available, followed by any custom tunings created within the I-1 or imported from a file format such as Scala (.scl), and finally, the base Custom Tuning, which can be used to build a custom tuning system entirely from scratch (don’t worry, this is not the only way to create a custom tuning).
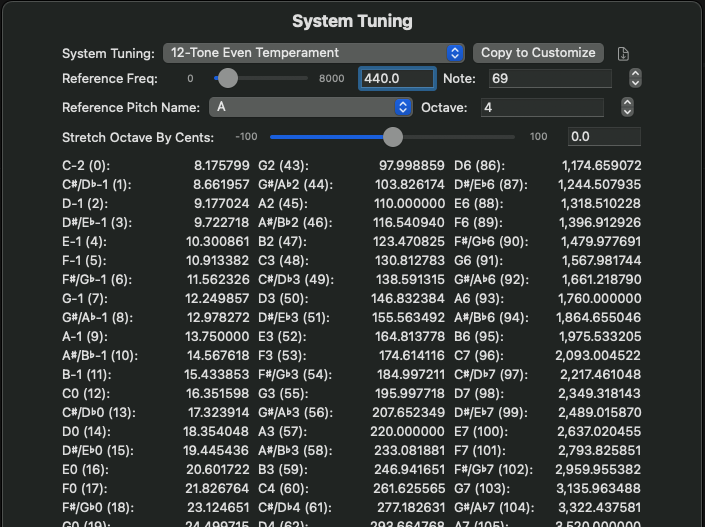
To the right of the drop-down, the Frequencies button will open a modal which shows the tunings frequencies and note names for 128 note numbers centered around the Reference Note. While MIDI 1.0 can only address 128 notes on a single channel, The Isle I-1’s internal engine views notes extending infinitely in either direction (well, practically infinite – it is limited to the min and max values of a 32-bit signed integer, but for notes that low, the frequency would be measured in days, while on the high end the frequencies would be way beyond any living creature’s hearing range). Finally, to the right of the Frequencies button, the Manage Tunings button allows you to manage the custom tunings present in the current Patch Bank – you can reorder them in any displayed lists, including tuning selection drop-downs (they will always appear after the canned tunings, this cannot be changed), rename or drop a custom tuning, and import or export Scala tuning files (.scl); Ableton’s extensions to the Scala format are supported in both directions.
Wait, what’s this about note numbers and frequencies? MIDI 1.0 sends Note On events, meaning, “play a note,” with a note number which tells you which key was played. All of the internal math, however, works with frequencies in Hertz. A note number indicates an action on a device; the tuning system converts that instruction into a frequency which can then be used by the engine. Most tunings create a 128-entry table of frequencies, indexed by note number. Some create more, as a 53-note scale (for example) would barely get 2 octaves’ worth of pitches into this tight a window. However, the engine uses a 32-bit signed integer to represent the note played. If you pass a note outside of the cache of frequencies, each tuning system can calculate the corresponding frequency. Thus, a note number of -2 billion might equate to a REALLY slow wave, but the engine can calculate it – it is unfazed by note numbers below zero, or note numbers greater than 127.
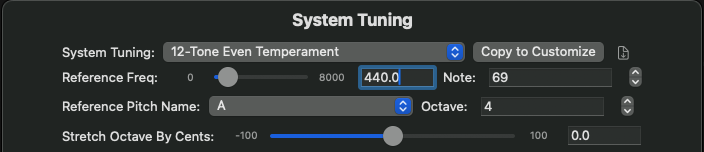
Several parameters are common to every tuning system – Reference Frequency and Reference Note define the origin of the tuning system. A tuning, custom or canned, typically starts with a reference frequency, then calculates the rest of the notes relative to this frequency. Reference Note defines where the first pitch in the scale, usually the reference frequency itself, resides on the instrument (as a note number). Reference Note Name and Reference Interval combine to define the note name of the first pitch. Available note names are defined by the tuning system, while interval is simply an integer value. For 12-Tone Equal Temperament, the default values are reference frequency of 440 Hz, on note number 69; note name is A, and interval is 4, combining to give a note name of A4.
Also common to all tuning systems is the ability to stretch the defining interval, usually (but not limited to) an octave. Stretched octaves are a common scenario in any tuning system, for a variety of reasons (in piano tuning, stretching an octave can make non-octave overtones sound more consonant and the overall tuning sound more “in-tune”). The slider for this parameter will adjust all active notes in real-time, relative to the stretched octave (non-octave notes will change pitch proportionately, and if a given note is below the reference frequency, you will actually hear the note DECREASE in pitch while the octave increases). The value is in units of cents (1/1200th of an octave), and ranges from -100 to +100 cents.
Many of the canned tuning algorithms carry additional parameters, which may also display here. The tuning-specific parameters will be described with each tuning system.
From the Frequencies panel, the same basic tuning parameters are available. The rightmost button past the Tuning drop-down is the Export to .scl button, which exports the selected tuning to a Scala (.scl) file. Many DAWs and other software read Scala tuning files, including Logic Pro and Ableton Live. Ableton defines their own extensions to this format, which the Isle I-1 also supports. Just to the right of the Tuning drop-down, the Copy to Customize button will copy the currently selected tuning to a new Custom Tuning – Custom Tunings will be described in full in the next section.
CUSTOM TUNINGS
There are three ways to create a Custom Tuning in the Isle I-1. The first, though not the easiest, is to select Custom Tuning from the Tuning drop-down – this creates a totally empty Custom Tuning, from which you can build a tuning from scratch. The second way is to import a Scala (.scl) tuning file. In addition to the base file format, the Isle I-1 supports Ableton’s extensions to the format, including reference frequency, reference note number, and note names. See https://www.huygens-fokker.org/scala/scl_format.html for a description of the base file format, and https://tuning.ableton.com/glossary/scala/ for a description of Ableton’s extensions. The third way to create a custom tuning is to copy another tuning via the Copy for Customization button on the Frequencies dialog. You can copy any of the canned tunings, as well as other custom tunings created via any of the 3 means. This is how you would map notes defined by a scale construction algorithm to keys (note numbers). For example, a 53-note scale is pretty unwieldy and a single octave occupies almost 2/3 of an 88-key piano keyboard. You may want to select only the notes you’re most likely to play and map them to a 12-key octave.
Tuning customization offers a whole host of features beyond just key mapping – you can construct an entire interval of equivalence, with each scale step defined as a ratio, in cents, or as degrees of an evenly divided octave (or other interval). The intervals above and below the definition will be filled out accordingly. You can customize the note names for this interval, build a tuning’s named intervals, reorder steps, insert steps, and eliminate others. You can also rename individual notes outside of the interval definition, assigning different note names in different octaves. Interval definition steps can be skipped in individual octaves; a single note can be inserted, totally outside of and independent from the interval definition. You can override the calculated frequency of a single note. And because so much of the work of tuning an instrument is done by ear, you can fine-tune the steps of an interval definition, or, if you prefer, a single note, in real time.
You can also use Custom Tunings to map different tuning configurations derived from the same canned tuning. If you wanted to use 12-Tone Equal Temperament at A-440 as the system tuning, but map a MIDI channel to 12-Tone Equal Temperament using C-264 as the reference frequency, click the Copy for Customization button, then change the reference frequency and reference note for the custom tuning. The custom tuning rebuilds the frequency table for this new copy, leaving the original intact.
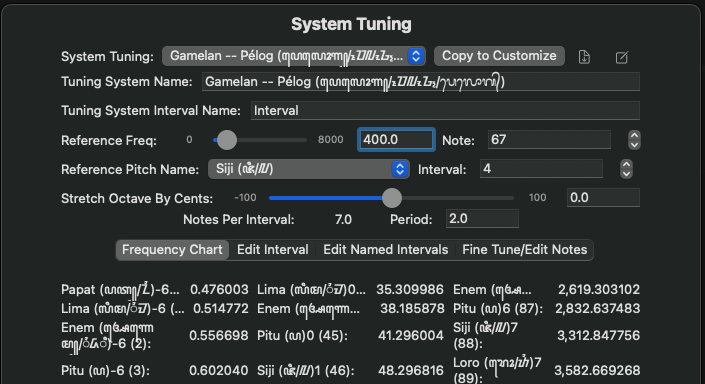
The Frequencies dialog, for a Custom Tuning, adds new controls and options to this panel. To the right of the Copy for Customization button, notice the Tuning Notes icon. While renaming your custom tuning is highly recommended, it is also highly recommended that the new name fit within the size of its edit box. Tuning Notes give you a place to spread out a little more, describing anything you feel is relevant to the tuning – where it came from, its reason for existing, anything you want to keep for future reference. The field accepts any Unicode character. The tuning notes are also included in the description line if you export this tuning to a Scala file.
Custom tunings allow editing of the Tuning System Name and Interval Name as well – you might want to refer to a non-octave interval by a different name, such as “Tritave” for a 3:1 interval.
Notes Per Interval are displayed, but not directly editable – this is the total number of steps in the interval definition, editing of which will be described shortly. The Period field is a 64-bit floating point number, defining the Interval of Equivalence as a ratio to the reference frequency; one octave would be a 2.0 ratio, a tritave would be a 3.0 ratio.
The Frequency Chart is now a tabbed display, showing the original list of frequencies plus 3 new edit options selectable from the pushbuttons along the top of the view.
Editing a Custom Tuning Interval
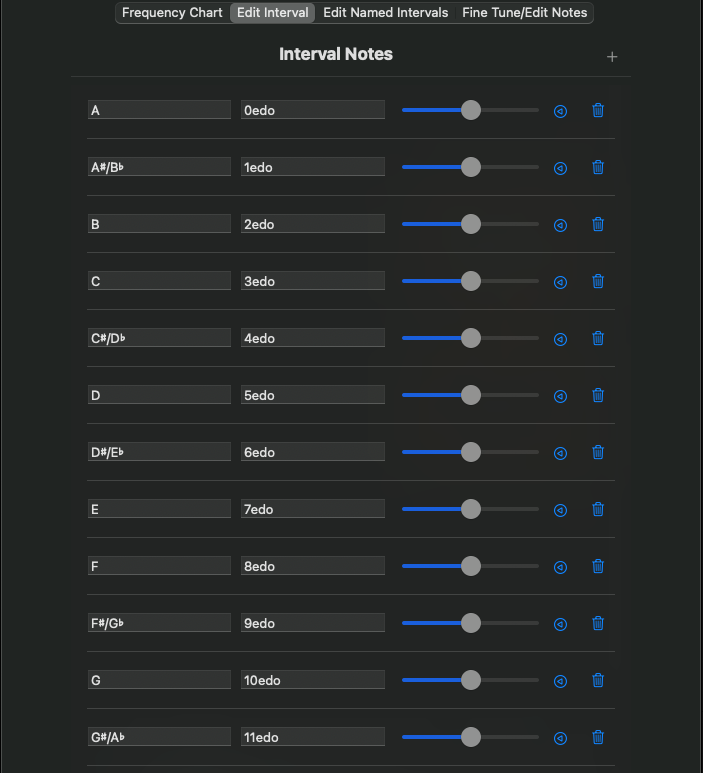
This panel defines the individual steps of a Period/Interval of Equivalence (these terms are interchangeable). They are defined relative to the reference frequency, and will be used to fill out intervals above and below the reference interval (the first interval, built with the steps applied to the original reference frequency). To add a scale step, click the + icon in the upper right corner of the table. The new step will be added to the end of the list. To reorder a step, drag and drop it into the desired position.
Each row defines a scale step. There is no limit to the number of scale steps you may define, however, there are practical limits to the number of scale steps a given instrument can cover, the number of scale steps a performer can track, and the requisite distance between two notes in order for a listener to be able to distinguish them. The first edit box defines the note name for the step, which can be any length and use any Unicode character. The second edit box defines the step in relation to the reference frequency. Valid formulae are:
- Ratio of 2 floating point values, with or without decimal points, separated by a forward slash (‘/’)
- A single floating-point value, with or without decimal point, in cents (a cent is 1/1200th of an octave, and by octave, I always mean a 2:1 ratio, regardless of the defined period of the tuning)
- A single step of notes-per-interval equal divisions of the defined period, specified by a single floating-point number followed by the characters “edo” (“equal division of the octave”). In this case, “edo” is used as a convention, even though it is an equal division of the defined period of the tuning, and not, strictly speaking, 1 octave. You are not limited to integer steps.
Invalid formulae will be chastised with an error message. The defined interval steps do not have to be in any order, nor do they have to fit within a single octave. This flexibility is a bit of a double-edged sword, as the I-1 will assume the defined order is intentional and will NOT sort the list, nor will it attempt to bring all notes into the same interval of equivalence.
To the right of the step formula is a slider for fine-tuning the scale step. The range of the fine-tuning is -100 cents to +100 cents, but there are no labels nor is the value displayed. This is intended to be used for fine-tuning by ear – any active sounds using this scale step will be adjusted in real time as you drag the slider. To reset the fine-tuning back to 0, click the Reset icon to the right of the slider.
Finally, if you wish to discard the scale step altogether, click the trash can icon.
Editing the Named Intervals
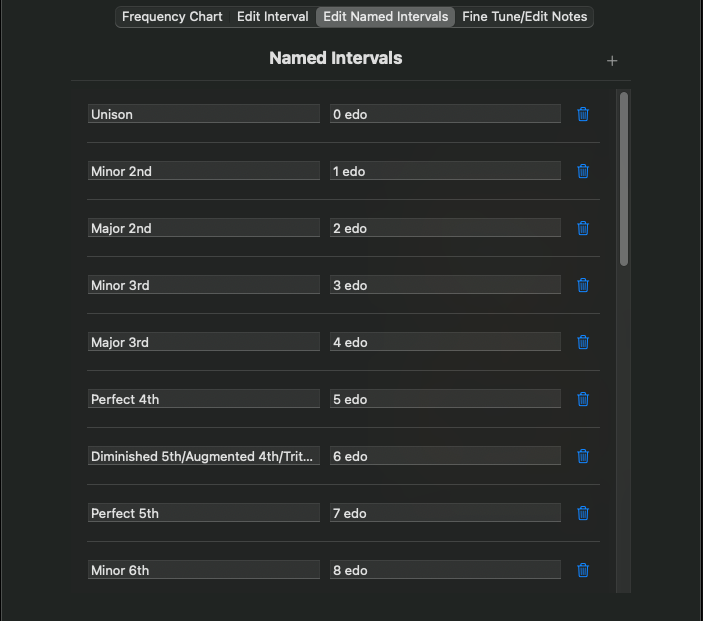
Most representations of frequency in the Isle I-1 allow you to specify that frequency in several different units/terms. One such term is the “Named Interval” – the distance between two pitches, plus a direction up or down. It is often more convenient/natural to say, “up a major 3rd,” than it is to express the same interval as a frequency ratio of 1.25; to change your mind and say, “no, wait, DOWN a major 3rd” than to invert the ratio in your head, and come up with a value of 0.8.
Named Intervals are defined by the tuning system, and a Custom Tuning allows you to define your own. If you copy an existing tuning, you will inherit the names of the original tuning as a starting point. You may remove a named interval by clicking the trash can icon on its line. Add a new interval by clicking the + icon in the table header. The two edit boxes allow you to specify an interval name (any Unicode character is accepted) and a formula. The formula has the same syntax as for scale steps – a ratio of floating point numbers separated by a forward slash; a single floating point value as a ratio in cents; or a step of an even distribution of the tuning’s defining interval, as a floating point number followed by the letters “edo”. For the ratio expression, you would generally define a ratio greater than or equal to 1, however, a ratio less than 1 is accepted; the only downside is that if you specify “up” a ratio less than 1, the resulting frequency will actually be in the “down” direction, and vice versa.
Fine Tune/Edit Notes
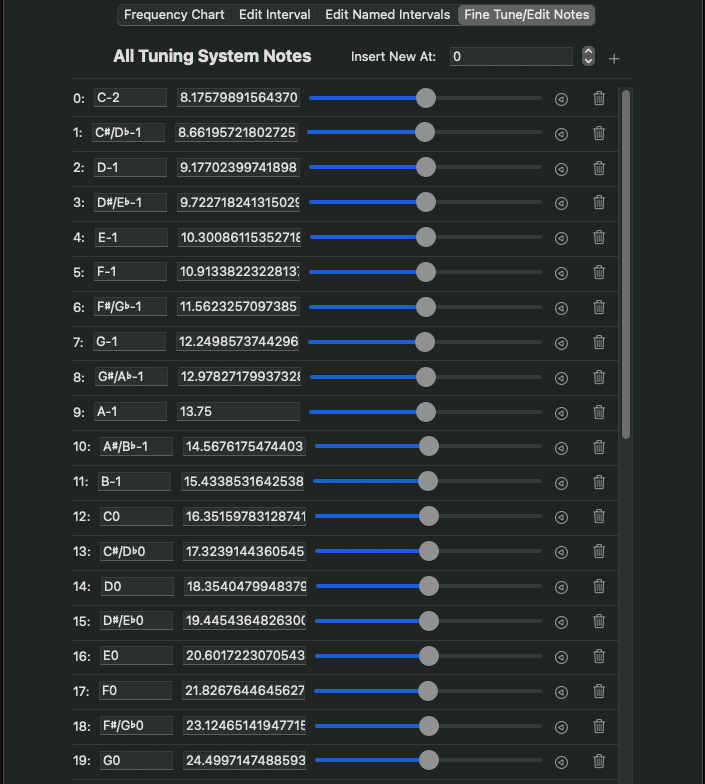
The Fine Tune/Edit Notes panel allows editing individual notes of the tuning. The list of available notes is initially filled out by the interval definition, repeated in both directions from the reference pitch/reference interval and centered such that 128 notes are displayed. A custom tuning defined as such is not limited to these 128 notes – if you passed the engine a note number outside of this range, the tuning will treat the defined notes as a 128-note scale with an interval definition of last note frequency divided by first note frequency, and calculate the requested note number accordingly. You may define more individual notes, and place them anywhere in the tuning – type the insertion point into the Insert New At: edit box, then click the + icon – a new note, with a frequency of 0 Hz, is inserted at the position, with a placeholder note name of “—“.
While this list doesn’t allow for reordering notes, user-added notes can be added and removed anywhere. Notes generated by the interval definition can be skipped in an individual occurrence. Remove or skip a note by clicking the trash can icon. Interval-defined notes are not actually removed, simply skipped; in this case, the line is gray, and the trash can icon turns into a recycle icon. Clicking the recycle icon “unskips” the skipped note. The leftmost column displays the note number of the note. Working to the right, the first edit box is the note name of that note; the generated note includes the interval number, so a tuning copied from 12-Tone Equal Temperament, set to A440 at note 69 and reference interval defined as 4, would show note 69 with a note name of “A4”. You can rename individual notes and override the names generated by the interval definition at that point. For example, you could rename note 60 to “Middle C”, and only the C at note 60 would carry that name – the C at note 48 would still be named “C3”. These names appear in the frequency chart and when selecting “Note” as the frequency unit in any frequency parameter. Any Unicode character is accepted. The second edit box overrides the calculated frequency generated by the named interval with a frequency value in Hertz. If you wanted to make a note play, for instance, 800 Hz in the middle of an octave ranging from 250-500 Hz, you create a sort of “pebble in the shoe” of your tuning. The frequencies are not required to be in ascending order from first to last note! Remember, a tuning is both scale construction AND note placement.
The slider in the middle of the row allows you to fine-tune individual notes of the tuning, with a range of -100 to +100 cents. The slider is not labelled, and does not display its value – this is meant to encourage fine-tuning by ear. Given that this is a piece of software, and furthermore that its author grew up in Western culture, it’s too easy to reduce a tuning to scale construction via mathematical ratios, but the reality of music practice over millenia and all over the world (including in Western traditions) is that so much of tuning is done by ear. Many systems of music are not defined by math – often a note is defined at a specific pitch for no other reason than, “that’s the way we’ve always done it here, make the instrument sound like the same note on the reference instrument.” Even in modern times, pianos are often tuned by ear, and stringed instruments such as guitars are almost always tuned by ear.
The fine-tuning for an individual note applies only to that specific note in the tuning. As a reminder, interval steps can also be fine-tuned (on the Edit Interval panel), and their fine-tunings are applied to every note they generate, across intervals/octaves. All tunings also support octave-stretching via slider, which may also be performed by ear.
If you want to start over with fine-tuning, click the Reset icon to the right of the slider.
Next — Isle I-1 User Guide – Appendix A – Index of Available Pre-Defined Tuning Algorithms
Previous — Isle I-1 User Guide — Chapter 7 — System-Level Objects, Performance-Only Mode, and MIDI 1.0

